PLC常用数制及转换方法，让你轻松掌握PLC编程

 一、什么是进位计数制

数制也称计数制,是指用一组固定的符号和统一的规则来表示数值的方法。按进位的原

则进行计数的方法,称为进位计数制。比如，在十进位计数制中,是按照“逢十进一”的原则进

行计数的。

常用进位计数制：

1、十进制(Decimalnotation)，有10个基数：0~~9，逢十进一；

2、二进制(Binarynotation)，有2个基数：0~~1，逢二进一；

3、八进制(Octalnotation)，有8个基数：0~~7，逢八进一；

4、十六进制数(Hexdecimalnotation)，有16个基数：0~~9，A，B，C，D，E，F

(A=10,B=11,C=12,D=13,E=14,F=15)，逢十六进一。

二、进位计数制的基数与位权

"基数"和"位权"是进位计数制的两个要素。

1、基数：

所谓基数，就是进位计数制的每位数上可能有的数码的个数。例如，十进制数每位上的数码，

有"0"、"1"、"3",…，"9"十个数码，所以基数为10。

2、位权：

所谓位权，是指一个数值的每一位上的数字的权值的大小。例如十进制数4567从低位到高

位的位权分别为100、101、102、103。因为：

4567＝4x103＋5x102＋6x101＋7x100

3、数的位权表示：

任何一种数制的数都可以表示成按位权展开的多项式之和。

比如：十进制数的435．05可表示为：

435．05＝4x102＋3x101＋5x100＋0x10－1＋5x10－2

位权表示法的特点是：每一项＝某位上的数字X基数的若干幂次；而幂次的大小由该数字所

在的位置决定。

三、二进制数

计算机中为何采用二进制：二进制运算简单、电路简单可靠、逻辑性强。

1、定义：

按“逢二进一”的原则进行计数，称为二进制数，即每位上计满2时向高位进一。

2、特点：

每个数的数位上只能是０，１两个数字；二进制数中最大数字是１，最小数字是０；基数为

２；

比如：10011010与00101011是两个二进制数。

3、二进制数的位权表示：

(1101.101)2＝1x23＋1x22＋0x21＋1x20＋1x2－1＋0x2－2＋1x2－3

4、二进制数的运算规则：

加法运算

①0＋0＝0③1＋1＝10

②0＋1＝1＋0＝1

乘法运算

①0×0＝0③1×1＝1

②0×1＝1×0＝0

四、八进制数

1、定义：

按“逢八进一”的原则进行计数，称为八进制数，即每位上计满8时向高位进一。

2、特点：

每个数的数位上只能是０、１、2、3、4、5、6、7八个数字；八进制数中最大数字是7，最

小数字是０；基数为8；

比如：(1347)8与(62435)8是两个八进制数。

3、八进制数的位权表示：

(107．13)8＝1x82＋0x81＋7x80＋1x8－1＋3x8－2

五、十六进制数

1、定义：

按“逢十六进一”的原则进行计数，称为十六进制数，即每位上计满16时向高位进一。

2、特点：

每个数的数位上只能是０、１、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六个数码；

十六进制数中最大数字是F，即15，最小数字是０；基数为16；

比如：(109)16与(2FDE)16是两个十六进制数。

3、十六进制数的位权表示：

(109．13)16＝1x162＋0x161＋9x160＋1x16－1＋3x16－2

(2FDE)16＝2x163＋15x162＋13x161＋14x160

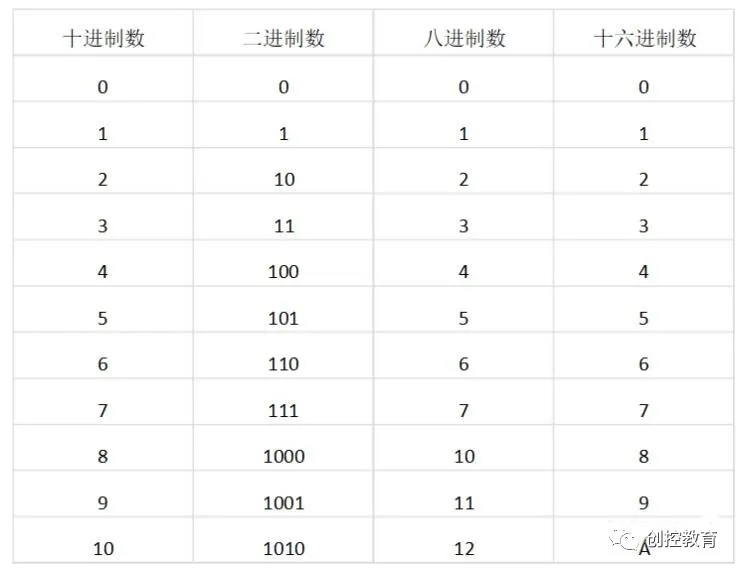
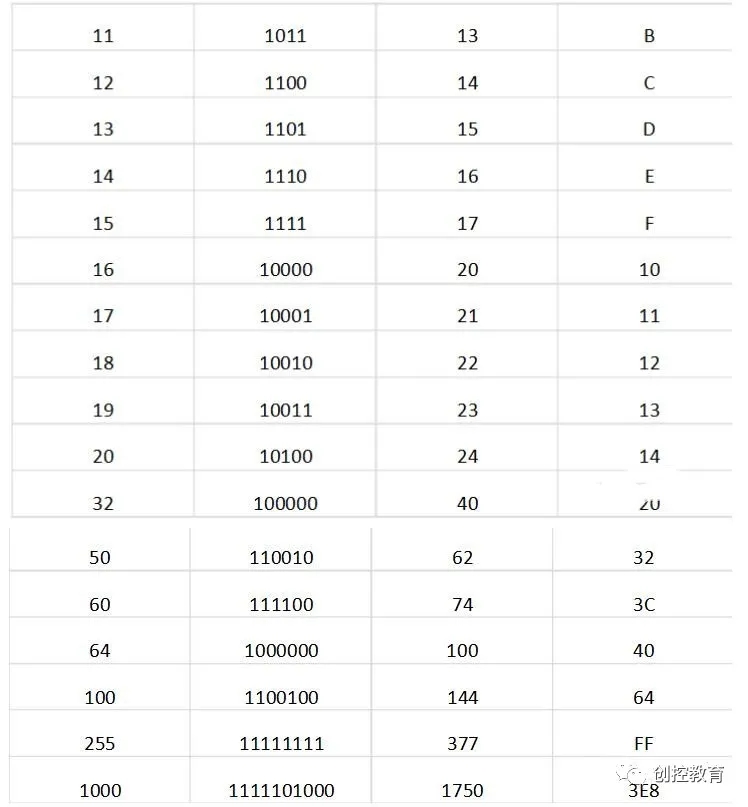
六、常用计数制间的对应关系

二进制数、八进制数、十六进制数及十进制数是现代数字系统中常用的四种数制，这几种进

位制计数制之间的对应关系如表1所列。

表1常用计数制数的表示方法

七、数制间的转换

1、十进制数转换成非十进制数

（1）十进制整数转换成非十进制整数

①为什么要进行数制间的转换？

将数由一种数制转换成另一种数制称为数制间的转换。

因为日常生活中经常使用的是十进制数，而在计算机中采用的是二进制数。所以在使用计算

机时就必须把输入的十进制数换算成计算机所能够接受的二进制数。计算机在运行结束后，

再把二进制数换算成人们所习惯的十进制数输出。这两个换算过程完全由计算机自动完成。

②转换方法

十进制整数化为非十进制整数采用“余数法”，即除基数取余数。

把十进制整数逐次用任意十制数的基数去除，一直到商是0为止，然后将所得到的余数由

下而上排列即可。

②十进制小数转换成非十进制小数转换方法

十进制小数转换成非十进制小数采用“进位法”，即乘基数取整数。

把十进制小数不断的用其它进制的基数去乘，直到小数的当前值等于0或满足所要求的精度

为止，最后所得到的积的整数部分由上而下排列即为所求。

2、非十进制数转换成十进制数

非十进制数转换成十制数采用“位权法”，即把各非十进制数按位权展开，然后求和。

3、二、八、十进制数之间转换

（1）二进制数与八进制数之间的转换转换方法

①把二进制数转换为八进制数时，按“三位并一位”的方法进行。

以小数点为界，将整数部分从右向左每三位一组，最高位不足三位时，添0补足三位；小数

部分从左向右，每三位一组，最低有效位不足三位时，添0补足三位。然后，将各组的三位

二进制数按权展开后相加，得到一位八进制数。

②将八进制数转换成二进数时，采用“一位拆三位”的方法进行。

即把八进制数每位上的数用相应的三位二进制数表示。

③二进制数与十六进制数之间的转换转换方法

a、把二进制数转换为十六进制数时，按“四位并一位”的方法进行。

以小数点为界，将整数部分从右向左每四位一组，最高位不足四位时，添0补足四位；小数

部分从左向右，每四位一组最低有效位不足四位时，添0补足四位。然后，将各组的四位二

进制数按权展开后相加，得到一位十六进制数。

b、将十六进制数转换成二进数时，采用“一位拆四位”的方法进行。

即把十六进制数每位上的数用相应的四位二进制数表示